La legge di gravitazione universale di Newton è una delle prime formule che si incontrano nel percorso di studi di Fisica. Questa semplice ed elegante legge descrive la causa del moto del 99% dei corpi che ci circondano.
Dalla caduta di un bicchiere, alle gocce di pioggia che danzano nel vento, fino alla meccanica di qualsiasi sport, la legge di gravitazione universale di Newton è un faro guida nella comprensione dei fenomeni che ci circondano. Il suo dominio non si ferma alla scala terrestre, ma si estende ai confini dell’universo, governando i moti celesti delle stelle e dei pianeti.
Il termine “universale” si cela nella matematica della legge: tutti i corpi esercitano la forza di gravità su tutti gli altri.
Cominciamo da una domanda: perché i corpi cadono a terra e non scelgono, invece, di andare verso l’alto o in una qualsiasi altra direzione?
Per rispondere è necessario comprendere la legge della gravitazione universale di Newton.
Nel 1687, sulla base degli studi condotti da Galilei e Keplero, Isaac Newton pubblica la legge di gravitazione universale:
\[
F=\frac{m_1 \cdot m_2}{r^2}G
\]
L’intensità della forza di gravità dipende dalle masse ($m_1,m_2$) dei corpi, cioè dalla quantità di materia presente in essi, e dalla distanza (r o R) che li separa. La masse rappresentano le sorgenti della gravità.
Le unità di misura della massa e della distanza sono rispettivamente kilogrammi (kg) e metri (m), mentre la forza si misura in newton (N).
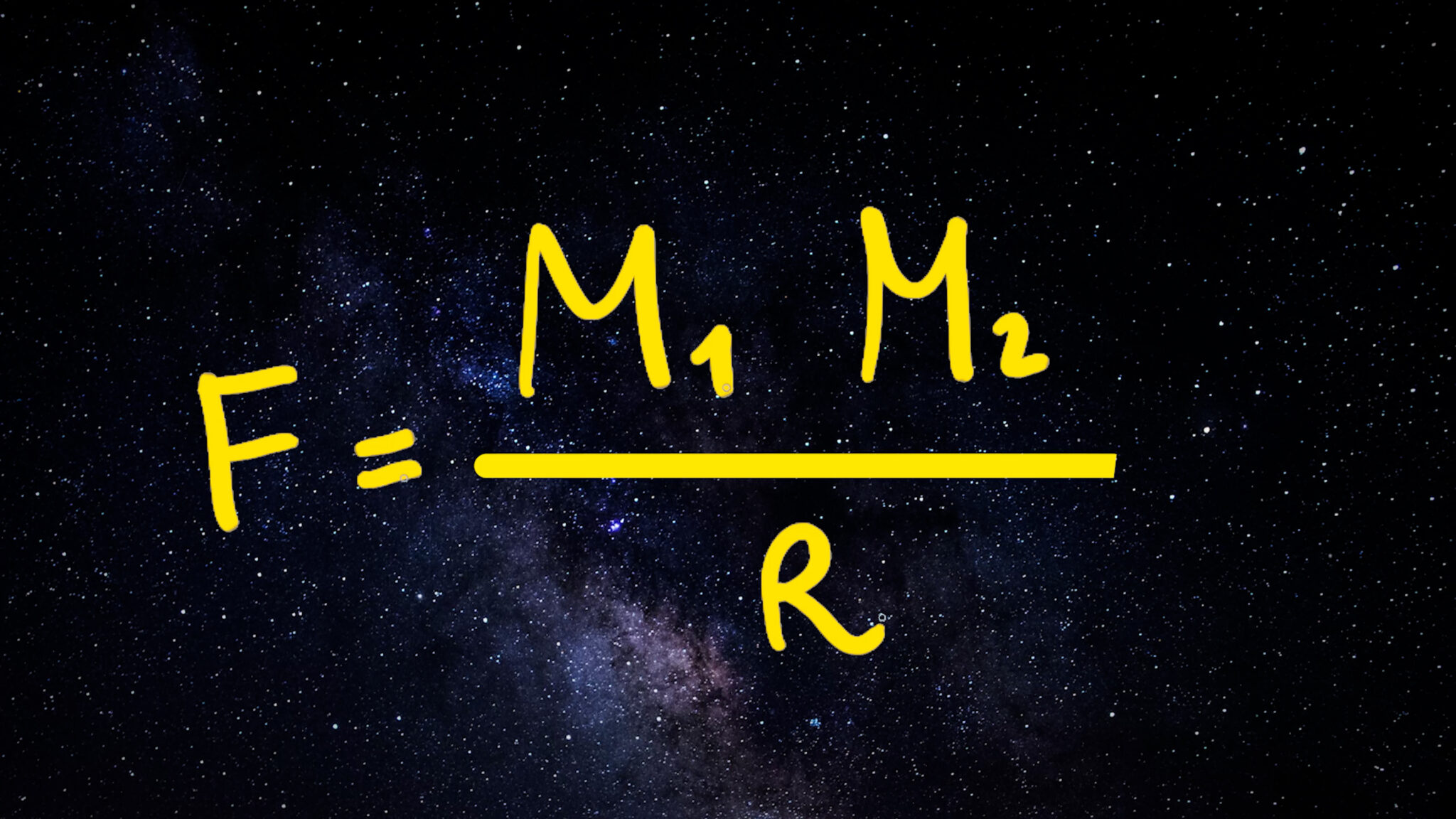
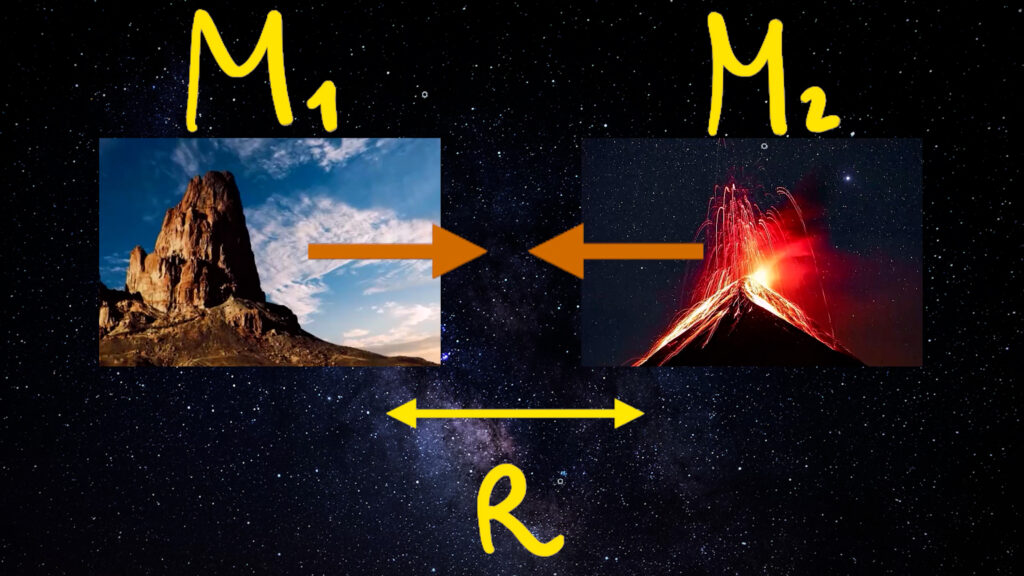
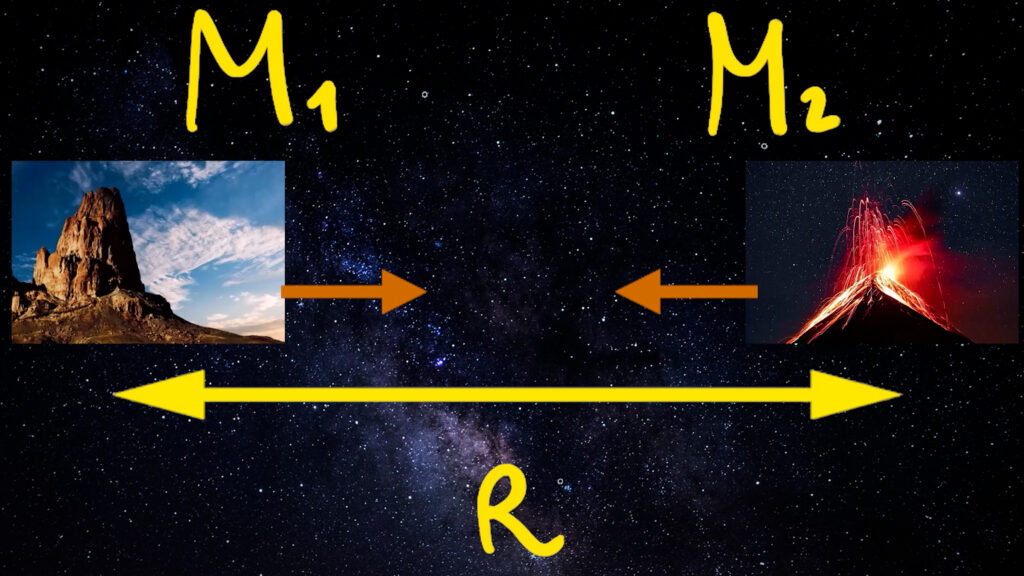
La formula della forza di gravità è data dal prodotto delle masse dei due corpi che consideriamo, diviso il quadrato della loro distanza. Raddoppiando la distanza, la forza diminuisce non di due, ma di quattro volte.
Infine, i tre termini vanno moltiplicati per una grandezza molto piccola, nota come costante di gravitazione universale di Newton, G, che indica l’intensità della forza di gravità, la più debole tra le 4 interazioni fondamentali che governano l’Universo.

Per il calcolo dell’unità di misura della costante di gravitazione G si suggerisce la visione del seguente breve video.
Per i corpi con cui interagiamo nel nostro quotidiano, anche se molto vicini, la forza di attrazione è trascurabile rispetto alle altre forze in gioco, come l’attrito con un pavimento.
Consideriamo due studenti, vicini di banco, che hanno la stessa massa di 50 kg e che si trovano ad una distanza di un metro.
Note le masse e la distanza, possiamo calcolare la forza di gravità con cui si attraggono, sostituendo i valori numerici nella formula:
\[
F=\frac{m_1 \cdot m_2}{r^2}G = \frac{50 kg \cdot 50 kg}{(1m)^2}G = 2500 \cdot G \frac{kg^2}{m^2}
\]
\[
G=6.67 \cdot 10^{-11} \frac{N m^2}{kg^2}
\]
\[
F=2500 \cdot 6.67 \cdot 10^{-11} \frac{N m^2}{kg^2} \frac{kg^2}{m^2} = 1.67 \cdot 10^{-7} N
\]
Si tenga presente che 1 newton è il peso esercitato da una massa di circa 100 grammi. La forza gravitazionale che si sviluppa tra due vicini di banco posti a un metro di distanza è circa un dieci milionesimo di Newton! L’intensità così bassa dipende dalle piccole masse in gioco, ma anche dal valore della costante di gravitazione universale.
Adesso consideriamo un caso in cui le masse sono più grandi e, di conseguenza, la gravità è più intensa!
Consideriamo il Sole e la Terra.
Dopo aver trovato (attraverso internet) il valore delle loro masse e della distanza (media, in quanto l’orbita è ellittica e non circolare) che li separa, sostituiamo i valori numerici nella formula:
\[
F=\frac{m_1 \cdot m_2}{r^2}G = \frac{5.98 \cdot 10^{24} kg \cdot 2 \cdot 10^{30} kg}{(1.5 \cdot 10^{11}m)^2}G
\]
\[
= 5.32 \cdot 10^{32} \cdot G \frac{kg^2}{m^2} = 3.55 \cdot 10^{22} N
\]
A differenza del caso precedente, la forza è enorme e, infatti, la Terra è vincolata ad orbitare attorno al Sole.
Curiosità:
Sostituendomi alla Terra nella formula, posso trovare la forza che il Sole esercita su di me. Approssimandomi ad una massa di 60 kg, per svolgere i conti più velocemente, la forza risulterà circa $10^{23}$ volte (centomila miliardi di miliardi di volte) più piccola rispetto a quella tra Sole e Terra.
\[
F \approx 0.1 N
\]
dieci volte inferiore rispetto al peso di una massa di circa 100 grammi.
Consideriamo il più semplice sistema atomico, l’idrogeno (H), che è composto da un protone e da un elettrone. La massa dell’atomo è data dalla somma delle masse dei suoi componenti.
Dopo aver trovato (sempre attraverso internet) i valori numerici, li inseriamo nella formula
\[
F=\frac{m_1 \cdot m_2}{r^2}G = \frac{1.67 \cdot 10^{-27} kg \cdot 10^{-30} kg}{(10^{-10}m)^2}G
\]
\[
= 1.67 \cdot 10^{-37} \cdot G \frac{kg^2}{m^2} \approx 10^{-47} N
\]
La forza di gravità all’interno dell’atomo di idrogeno è infinitamente piccola rispetto agli scenari precedentemente considerati, infatti l’atomo è tenuto assieme da forze di natura elettromagnetica e non gravitazionale.
Riassumendo, tutti i corpi nell’universo esercitano la forza di gravità su tutti gli altri.
In questo istante, siamo soggetti ad un’attrazione da ogni direzione, non solo dai corpi che si trovano vicini, ma anche dalle stelle nelle galassie più remote. La prossima domanda a cui risponderemo emerge di conseguenza:
qual è la massa che genera la forza più significativa su di noi?
Prima di passare al prossimo articolo, ti propongo un veloce quiz per verificare le conoscenze acquisite.



Add a Comment