Il moto di caduta libera è il moto più frequente nell’universo: da un bicchiere che cade, al colossale agglomerato di stelle e pianeti che cadono gli uni verso gli altri.
Il principio è sempre il medesimo: tutti i corpi nell’universo esercitano la forza di gravità su tutti gli altri. Per comprendere il tipo di movimento che ne scaturisce, dobbiamo aggiungere due ingredienti cruciali:
- Un’equazione del moto
- La velocità iniziale dei corpi che cadono
L’obiettivo di questo articolo è capire perché i corpi cadono a terra e non scelgono, invece, di andare verso l’alto o in una qualsiasi altra direzione.
Nel 1687, Newton non pubblica solo la legge di gravitazione universale, ma anche tre leggi sul moto dei corpi: i principi della dinamica.
Nello scorso articolo, abbiamo visto che la Terra esercita la forza peso su un qualsiasi corpo sulla sua superficie. Per esempio, una mela appesa ad un ramo, in ogni istante, si sentirà attratta verso il centro della Terra con una forza pari al suo peso,
\[
F=m \cdot g
\]
dove m è la massa della mela e g è l’accelerazione di gravità sul pianeta Terra, $9.81 \frac{m}{s^2}$. Ricordo che l’accelerazione g dipende dalla massa e dal raggio (al quadrato) del corpo celeste su cui ci si trova.
La domanda è la seguente: se la Terra esercita il peso sulla mela, che forza esercita la mela sulla Terra?
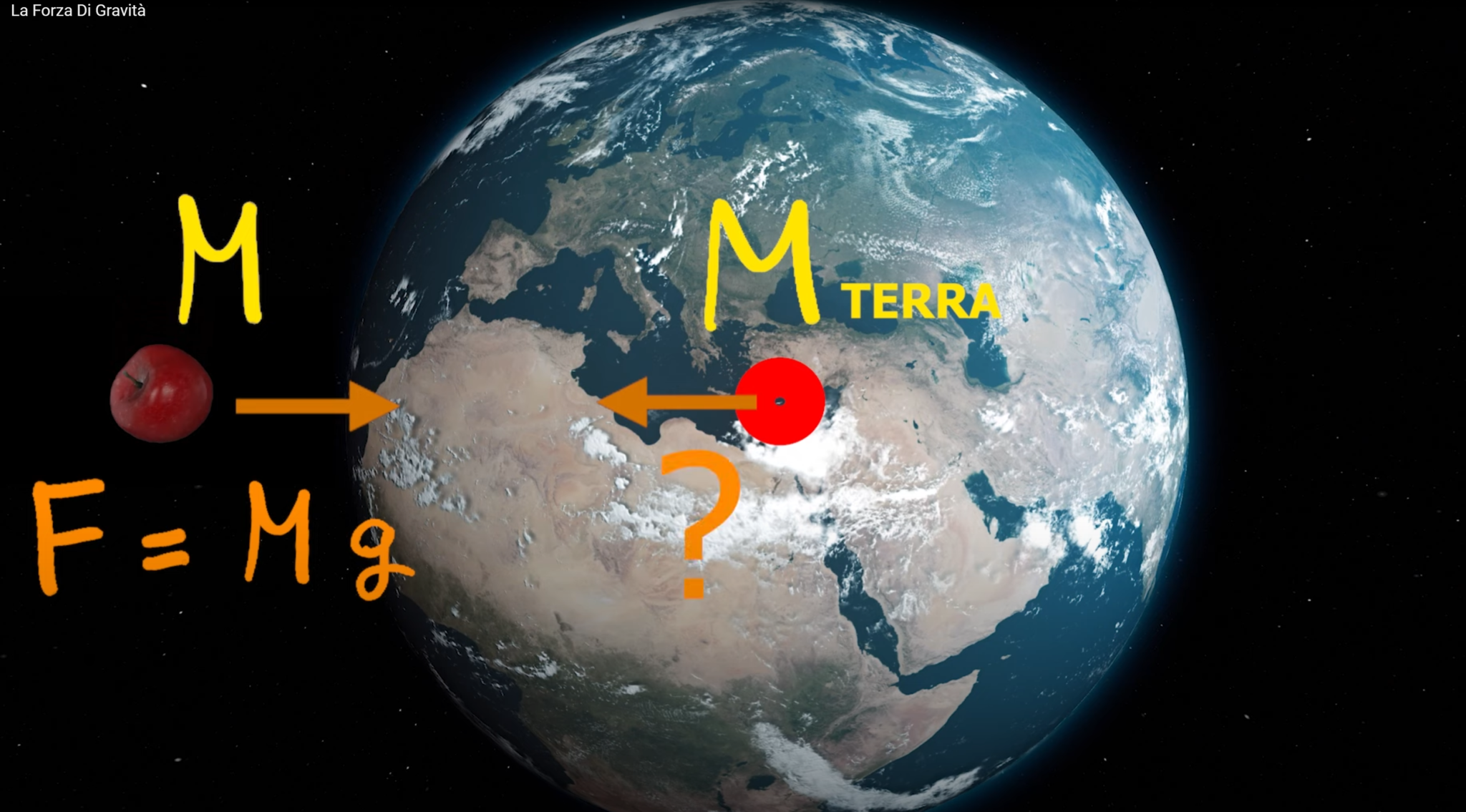
Istintivamente siamo portati a pensare che la mela eserciti sulla Terra una forza pressoché nulla. In realtà, la forza è la stessa: il peso della mela.
La matematica ci viene in soccorso: guardando la formula, non potrebbe essere altrimenti, essendo presenti entrambe le masse!
La forza è
\[
F=m \cdot g = \frac{m_{mela} \cdot m_{Terra}}{R_{Terra}}G
\]
E’ giunto il momento di introdurre la formula che ha consacrato Newton pioniere della Fisica: forza uguale massa per accelerazione, il secondo principio.
\[
F= m \cdot a
\]
Il secondo principio della dinamica di Newton ci dice che esercitando una forza F su un corpo di massa m questo accelera con a.

Tornando al nostro esempio, la Terra esercita la forza peso sulla mela. Se il ramo che la tiene sospesa si spezza, la mela inizierà a muoversi accelerando verso il basso in un moto di caduta verticale.
Per trovare l’accelerazione con cui cade la mela, si sostituisce ad F nel secondo principio la forza di gravità che la mela subisce,
\[
F = m \cdot a = m \cdot g \rightarrow a = g
\]
Semplificando la massa, che è la stessa (della mela) in entrambi i membri dell’equazione, si ottiene l’accelerazione esercitata dalla gravità della Terra sulla mela, che infatti coincide con l’accelerazione di gravità terrestre!
Tutti i corpi cadono con la stessa accelerazione
Galileo lo aveva capito, dopo aver svolto vari esperimenti, pur non disponendo del potente apparato matematico formulato da Newton.
Il secondo principio della dinamica di Newton non è una semplice equazione, bensì un’equazione differenziale. La soluzione di un’equazione semplice è un numero (come 5 o $\pi$). La soluzione di un’equazione differenziale è una funzione, una traiettoria nel caso sotto esame.
Immagina l’equazione come un racconto matematico (da risolvere e svelare) che rivela il percorso seguito da un corpo nel suo viaggio attraverso lo spazio e il tempo.
Per esplorare questo concetto in modo più approfondito, si suggerisce la visione del seguente breve video che tratta il caso specifico di un corpo in caduta libera verticale.
Attenzione, una piuma che viene fatta cadere nel vuoto risponde esattamente alla trattazione svolta finora. Se invece la piuma viene fatta cadere in presenza di un mezzo come l’aria, agiscono su di essa altre forze che ne alterano completamente la dinamica, impedendole di cadere con la stessa velocità che aveva accumulato nel vuoto, soggetta alla sola forza peso.
Cosa succederebbe alla mela, se si trovasse lontano dalla Terra e da altri corpi celesti?
Dato che la forza dipende dalla distanza,
\[
F=\frac{m_1 \cdot m_2}{r^2}G
\]
man mano che allontaniamo la mela dalla Terra, la forza (o il suo peso) continua a diminuire fino ad annullarsi. Una volta che ci si trova sufficientemente lontano da corpi celesti, possiamo assumere che la forza sia nulla.
In assenza di forze si sostituisce F=0 nel secondo principio, ottenendo un’accelerazione nulla
\[
F= m a = 0 \rightarrow a = 0
\]
L’accelerazione è la variazione di velocità nel tempo, ciò significa che in assenza di forze la velocità di un corpo è costante.

Riassumendo, una mela in caduta libera, soggetta alla forza di gravità della Terra, esercita sulla Terra la stessa identica forza. Tuttavia, è la mela a cadere verso la Terra e non viceversa, in quanto la sua massa è molto più piccola.
In presenza della sola forza di gravità, tutti i corpi cadono a terra con la stessa accelerazione, indipendentemente dalla loro massa.
In assenza di forze, un corpo si muove a velocità costante.
Per consolidare le conoscenze acquisite, si propone lo svolgimento di un breve quiz!



Add a Comment