In misura diversa, tutti i corpi esercitano la forza di gravità su tutti gli altri. Qual è il corpo che genera la forza di gravità più importante su di noi?
Premesso che la costante di gravitazione è sempre uguale ($G=6.67\cdot 10^{-11} \frac{Nm^2}{kg^2}$), la legge di gravitazione universale
\[
F=\frac{m_1 \cdot m_2}{r^2}G
\]
ci suggerisce che, per produrre una forza gravitazionale significativa, le masse in gioco devono essere sufficientemente grandi da compensare il valore della costante di gravitazione universale. Ad esempio, se $m_1$ sono io, per ottenere un valore significativo di gravità, $m_2$ dovrà essere una massa di ordine del Sole ($m=10^{30}kg$) o ancora maggiore, tipo un buco nero o una galassia.

Attenzione, non dobbiamo dimenticare che la forza dipende anche dalla distanza tra i due corpi! Ciò implica che, per rispondere al quesito iniziale, dobbiamo trovare un corpo massivo e relativamente vicino. Il compromesso tra massa e distanza, per noi, è garantito dalla Terra, che ha una massa un milione di volte inferiore al Sole, ma una distanza tra noi e il suo centro di soli 6371 km, rispetto ai 150 milioni di km con il Sole!

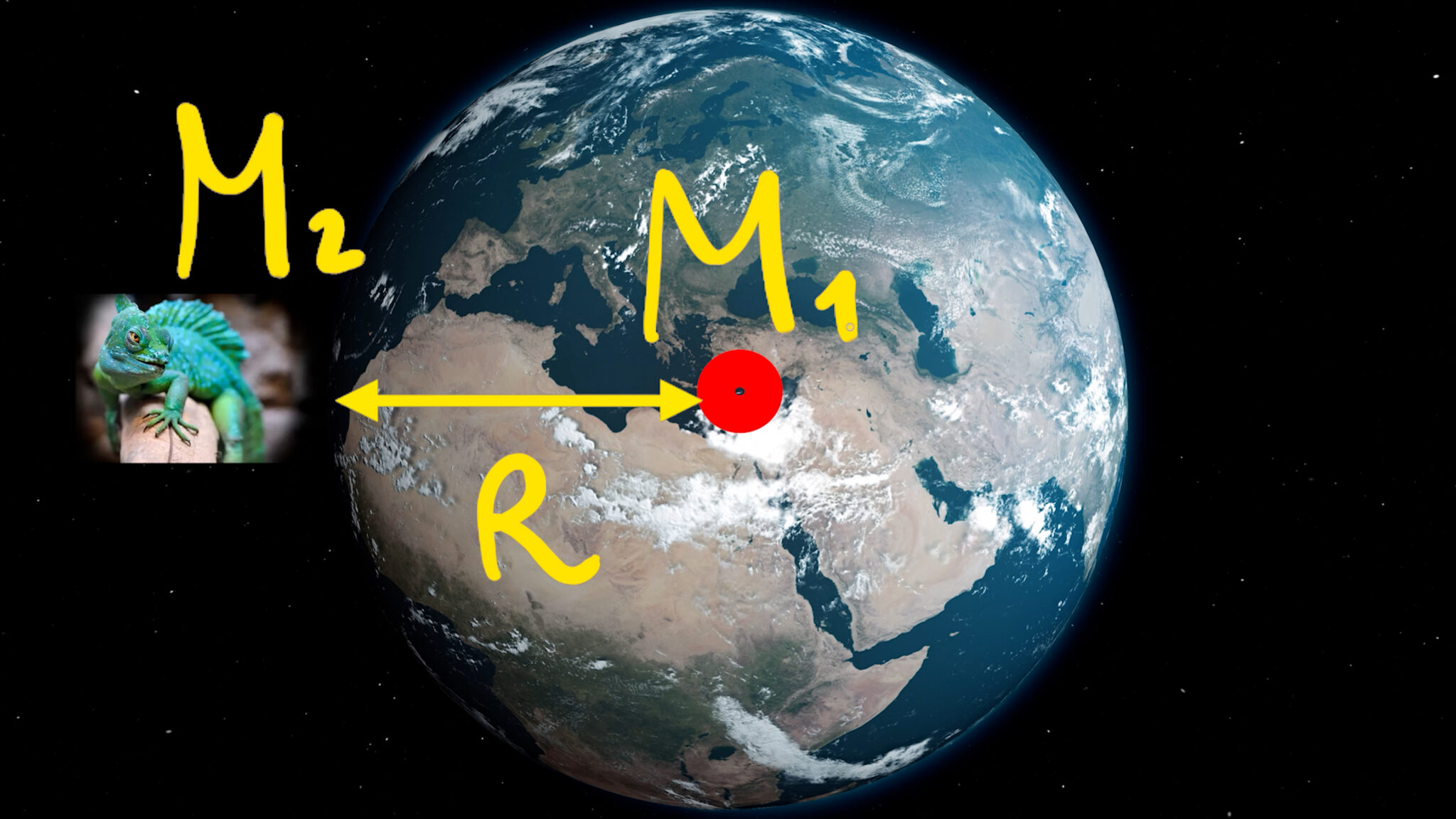
Approssimando, per semplicità, la Terra ad una sfera, la distanza tra un qualsiasi corpo sulla sua superficie e la Terra sarà sempre il raggio della Terra!
La massa del corpo la lasciamo generica, indicandola con “$m_1$”. Inserendo i valori di massa e raggio della Terra nella formula, si trova la forza di gravità
\[
F=\frac{m_1 \cdot m_2}{r^2}G = \frac{m_1 \cdot 5.98 \cdot 10^{24} kg}{(6.37 \cdot 10^6 m)^2} G = m_1 \cdot 9.81 \frac{m}{s^2}
\]
dove $9.81 \frac{m}{s^2}$ è il valore dell’accelerazione di gravità terrestre e si indica con “g”. La g dipende dalla massa e dal raggio della Terra e dalla costante di gravitazione universale.
Abbiamo trovato il peso di un corpo di massa $m_1$ sulla superficie della Terra!
\[
F=\frac{m_1 \cdot m_T}{r_T^2}G = m_1 \cdot 9.81 \frac{m}{s^2} = m_1 \cdot g = P
\]
Il peso è la forza di gravità che un corpo subisce sulla superficie della Terra.
Cosa misura realmente una bilancia?
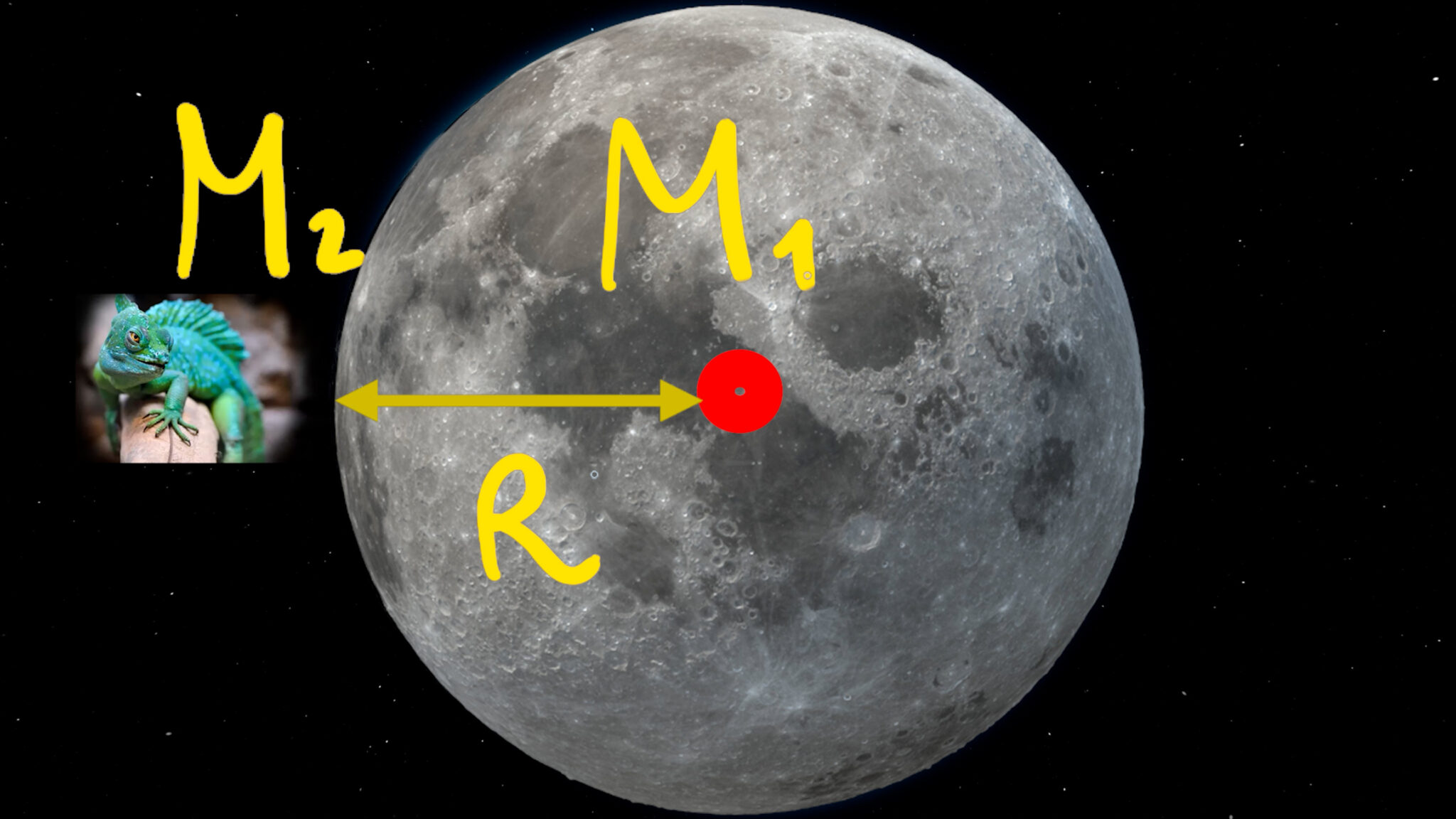
\[
F=\frac{m_1 \cdot m_2}{r^2}G = m_1 \cdot g = m_1 \cdot 1.62 \frac{m}{s^2}
\]
si ottiene che l’accelerazione di gravità sulla superficie lunare (e quindi il peso sulla Luna) è circa un sesto di quella terrestre.
Per questo motivo, sulla Luna i movimenti sono più “ampi” e “lenti”. Per esempio, a parità di lunghezza del filo, un pendolo ci mette più tempo a compiere un’oscillazione completa sulla Luna che sulla Terra. Per la stessa ragione, un carico di 100kg sulla Luna richiederà un sesto della forza impiegata sulla Terra per essere sollevato.
Saremmo tutti campioni, sulla Luna!
Lo stesso identico ragionamento si può applicare al Sole, a cambiare saranno solo la massa e il raggio.
Per un qualsiasi corpo sulla superficie solare la forza gravitazionale più importante arriva dal Sole.
\[
F=\frac{m_1 \cdot m_2}{r^2}G = m_1 \cdot 274 \frac{m}{s^2}
\]
A differenza del caso precedente, l’accelerazione (e di conseguenza la forza peso) è quasi 30 volte maggiore di quella terrestre.
Pertanto, un pendolo ci metterà meno ad oscillare sulla superficie del Sole, come un oggetto a cadere. La forza necessaria per sollevare una massa di 100kg diventa quasi 30 volte maggiore che sulla Terra.
Sei al sushi e ti bullizzano, dicendoti che mangi così tanto da generare un campo gravitazionale significativo nelle vicinanze? Dimostriamo che è una baggianata.
Supponiamo una massa esagerata, diciamo quella di un piccolo ippopotamo: 1000 kg. Chiediamoci quale accelerazione di gravità genera una massa di 1000kg su una massa $m_1$ generica a un metro di distanza. Inserendo i valori, si trova
\[
F=\frac{m_1 \cdot m_2}{r^2}G = \frac{m_1 \cdot 1000 kg}{(1m)^2}G \approx m_1\cdot 10^{-7} \frac{m}{s^2}
\]
Immaginando di essere nello spazio vuoto in assenza di altre forze, cadremmo verso l’ippopotamo con un’accelerazione che comporta un aumento di velocità di un diecimilionesimo di metro al secondo ogni secondo. Una massa di 1000kg, dunque, non riesce a generare un campo gravitazionale sufficiente a caderci dentro.
Riassumendo, tutti i corpi nell’universo esercitano la forza di gravità su tutti gli altri. La forza più importante, la subiamo dalla Terra e coincide con il nostro peso!
Il nostro pianeta è il principale artefice della nostra esperienza quotidiana di peso. È la Terra che attira ogni oggetto verso il suo centro con una forza che chiamiamo gravità. Questo legame invisibile è ciò che ci fa sentire ancorati al suolo, influenzando ogni passo, ogni salto e ogni lancio di pallone.
Per verificare le conoscenze acquisite prova a svolgere il quiz!



Add a Comment